Aria triunghiului isoscel | Meticulos, simplificat, explicații vizuale
Invață matematică online, cu profesor. Meticulos, simplificat, explicații vizuale. Intră pe site sau întreaba-ne detalii: office@accesis.ro
Triunghiul isoscel are prin definitie doua laturi congruente si o baza. Unghiurile si liniile importante sunt: mediana, mediatoare, bisectoare și înălțime. Calculul Ariei
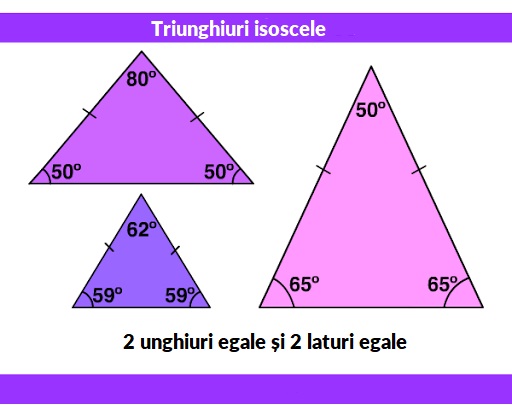
Teorema: intr-un triunghi isoscel, unghiurile alaturate bazei sunt congruente.
Reciproca teoremei: daca un triunghi are doar doua unghiuri congruente atunci el este isoscel.
Intr-un triunghi isoscel mediana corespunzatoare bazei este si mediatoare si bisectoare si inaltime. OBS: Daca o linie importanta este mediatoare, este suficienta pentru ca triunghiul sa fie isoscel. Asta pentru ca mediatoarea trece prin mijlocul segmentului (este mediana) si este perpendiculara pe segment (este inaltime)
Prin coborîrea înălţimii, în triunghiul isoscel cu catetele egale se formează două triunghiuri dreptunghice (au câte un unghi drept, de 90 grade) perfect egale. ( laturi, unghiuri şi arii) În triunghiul dreptunghic fiecare catetă este egală cu media geometrică dintre ipotenuză și proiecția catetei pe ipotenuză.
Pentru a afla aria unui triunghi isoscel vom calcula intai aria unuia dintre triunghiurile dreptunghice formate prin coborîrea înălţimii.

Pregateste-te la matematica cu profesor online. Intra pe pagina
Într-un triunghi dreptunghic (triunghiul care are un unghi drept, de 90 grade) lungimea înălțimii corespunzătoare ipotenuzei (ipotenuza = latura opusa unghiului de 90 de grade) este egală cu media geometrică a lungimilor proiecțiilor catetelor (celelalte 2 laturi) pe ipotenuză.
Lungimea înălțimii in triunghiul dreptunghic se calculeaza astfel = √(x · 4x) = √(4x²) = 2x
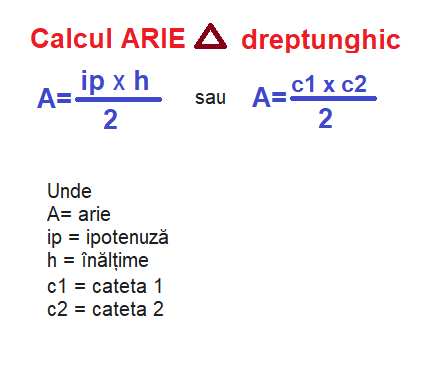
Aria într-un triunghi dreptunghic este egală cu semiprodusul catetelor sau semiprodusul dintre ipotenuza si inaltime.
Aplicarea Teoremei Lui Pitagora La Triunghiul Isoscel
Teorema lui Pitagora: „suma pătratelor lungimilor catetelor este egală cu pătratul lungimii ipotenuzei”. Aceasta poate fi reprezentată în triunghiul dreptunghic ABC, AB fiind ipotenuza, iar C unghiul drept.
Teorema lui Pitagora spune că:
Pentru un triunghi isoscel oarecare (cu unghiul dintre catete diferit de 90) pentru calcularea ariei putem folosi doar Teorema lui Pitagora. Prin teorema lui Pitagora aflăm dimensiunea înălţimii. Apoi aplicăm formula ariei triunghiului, b x h / 2 (baza ori înălţimea supra 2).
Teorema catetei
În triunghiul dreptunghic fiecare catetă este egală cu media geometrică dintre ipotenuză și proiecția catetei pe ipotenuză. Fie triunghiul ABC cu C=90° și CD perpendiculara pe AB. Există relația:

Fie ABC un triunghi oarecare și a, b, c lungimile laturilor [BC], [AC], respectiv [AB]. Aria triunghiului ABC poate fi calculată cu una din formulele: A_ABC=(a⋅b⋅sin∡C)/2 = (a⋅c⋅sin∡B)/2 = (b⋅c⋅sin∡A)/2 .
Vrei sa inveti rapid la matematica? Pregateste-te cu noi online. Intra pe pagina





