Progresie geometrică și aritmetică – explicații, formule, figuri
În această mini-lectie, vom explora lumea progresiei aritmetice și a progresiei geometrice în matematică. Veți învăța despre formula de progresie aritmetică, formula de progresie geometrică și alte lucruri interesante în jurul acestui subiect.
Deseori întâlnim cuvântul „ secvență ” în viața noastră de zi cu zi. Să începem prin a răspunde la o întrebare simplă. Ați observat vreodată tipare în viața de zi cu zi?
De exemplu, niște copii din autobuz, în timp ce merg spre casă, observă un model de numere de case pe stradă. Aceste numere sunt în ordine crescatoare. Aceste numere de case formează o secvență.
Pregătește-te online la matematică. Pentru detalii si costuri viziteaza site.

Să mergem mai departe și să învățăm despre două tipuri de secvențe: progresia (secvența) aritmetică și progresia (secvența) geometrică.
Definiția progresiei aritmetice și a progresiei geometrice.
PROGRESIA ARITMETICĂ
O progresie aritmetică este o SUCCESIUNE / SECVENTA de numere în care fiecare termen succesiv este o sumă a termenului său precedent și a unui număr fix. O secvență poate fi definită ca o aranjare adecvată a ceva anume într-un anumit model sau ordine. Acest număr fix se numește diferență comună.
Progresia aritmetică (PA) – Într-o progresie aritmetică, diferența dintre cei doi termeni consecutivi este întotdeauna aceeași. Cu alte cuvinte, este o succesiune în care fiecare termen crește sau scade cu o constantă fixă. Diferența fixă dintre termenii consecutivi se numește „ diferența comună ” a progresiei aritmetice. Se notează cu „d”.
Este de remarcat că această diferență poate fi pozitivă, negativă sau zero .

Fiecare număr din progresia aritmetică se numește termen.
Într-o progresie aritmetică, dacă „a” este primul termen și „d” este diferența comună, atunci
forma generală a unei progresii aritmetice este dată de,
a, a+d, a+2d, a+3d,….
De asemenea, dacă A1, A2, A3,….An sunt în PA, atunci diferența comună d este dată de
d=A2–A1 =A3–A2 =A4–A3=……=An–An – 1
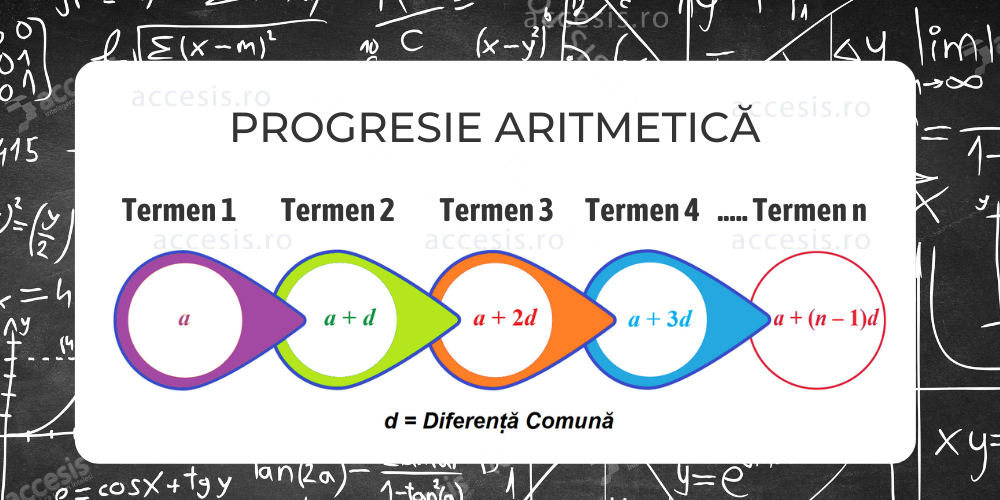
Când există un număr definit de termeni într-o progresie aritmetică, atunci se numește progresie aritmetică finită.
Mai mult, dacă există un număr nedefinit de termeni într-o progresie aritmetică, atunci se numește progresie aritmetică infinită.
al n-lea termen al unei progresii aritmetice (PA):
Când într-o serie aritmetică finită-
„a” este primul termen
„d” este diferența comună
„l” este ultimul termen
An este al n-lea termen al PA
Prin urmare,
| al n-lea termen al progresiei aritmetice este dat de- An = a + (n-1) d |
Al n-lea termen este formula explicită a secvenței aritmetice și poate fi util pentru a găsi orice termen al progresiei. suma progresiei aritmetice
Meditații matematică online, cu profesor. Detalii pe site.
PROGRESIA GEOMETRICĂ
Progresia geometrică este o serie de numere diferite de zero, în care fiecare număr după primul număr poate fi găsit prin înmulțirea numărului imediat precedent cu o constantă.
Pe scurt, o secvență A1, A2, A3,… An se numește progresie geometrică dacă fiecare termen este diferit de zero – fractia Ak + 1 / Ak = r(constant) pentru k ≥ 1.
Forma generală a unei Progresii Geometrice este dată de a, ar, a r2, a r3, . . . unde
a= primul termen al progresiei geometrice
r = raport comun
Fie primul termen al secvenței A iar raportul comun să fie r.
Atunci, n al termenul șirului este dat de:
| An=Arn−1 |
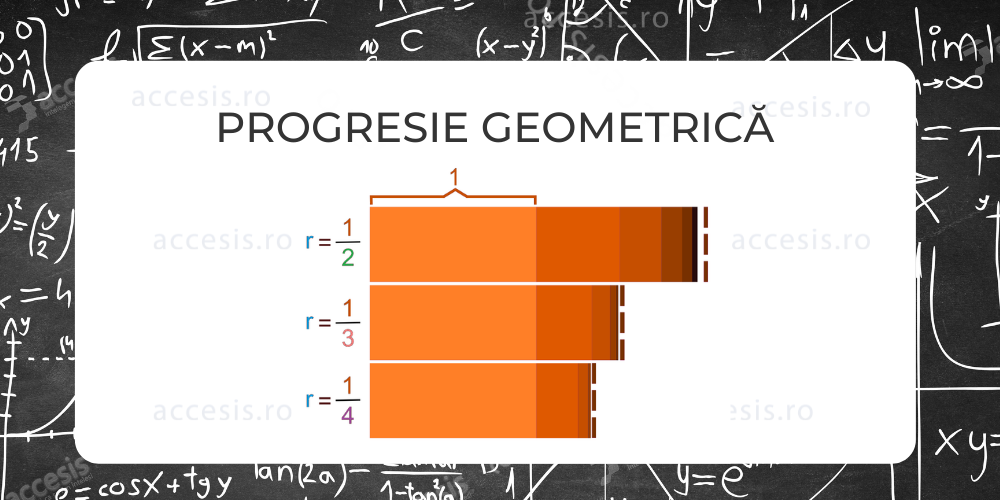
Raport comun (r) – În PG, fiecare termen, cu excepția primului termen, are un raport constant față de termenul său imediat. Acest raport constant se numește „raport comun” al GP
Să presupunem, A1, A2, A3, …,}An sunt in PG
atunci raportul comun(r) =A1/A2=A2/A3=A3/A4=…=An – 1An
De exemplu: 12, 24, 48, 96,… sunt în progresie geometrică
, atunci r =12/24= 2
de asemenea, r =24/48= 2
și așa mai departe.
al n-lea termen al unei progresii geometrice
Dacă „a” este primul termen și „r” este raportul comun
, atunci, al n-lea termen al unui PG este dat de-
| An =arn-1 |
Intra pe site pentru meditatii online cu profesor
Note importante
- Într-o progresie aritmetică, fiecare termen succesiv se obține prin adăugarea diferenței comune la termenul său precedent.
- Într-o progresie geometrică, fiecare termen succesiv se obține prin înmulțirea raportului comun cu termenul său precedent.
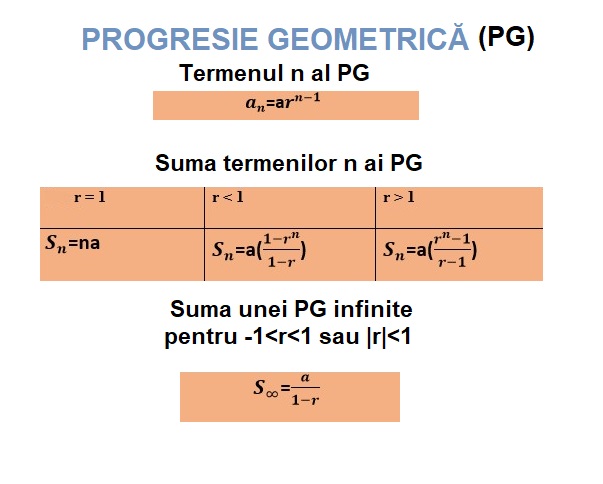
- Suma progresiei aritmetice al cărei prim termen este A iar diferența comună este d poate fi calculat folosind una dintre următoarele formule:
Sn=n/2 (2A+(n−1)d) Sn=n/2 (A1+An) - Suma progresiei geometrice al cărei prim termen este A iar raportul comun este r poate fi calculat folosind formula:
Sn=A(1−rn) / 1−r
In aceasta figura poti vedea diferenta intre secvențele aritmetice și cele geometrice




